数学の勉強方法
1.【チャート式参考書】数学力が一生伸びない間違った青チャートの使い方 とん
1.青チャ-トの使い方を間違わない。この参考書は辞書であるので解いていこうとしない。分量的にしない方がいい。効率的にやる。わからないところをやる方がいい。いつまでも終わらない。何周すればいいか?そんな必要はない。数学は考えるところにある。パタ-ン暗記で通用するのは中堅レベルまで。1回きちんと解いて理解していれば記憶に定着する。難関大学を目指す人は考えることをしてほしい。これが数学。簡単に解答をみてはいけない。解答を読んで満足してはいけない。記述力を高めるためにためには写経すること。解答を写すことで数学力が上がる。数学の記述が重要。
2.「受験数学は基礎が大事」って言うけど基礎って何や?数学科生が解説 とん
基礎とは何か?基礎レベルの問題が解けるかとかいうことでない。自分なりの方法で解答したらいい点の時と悪い時の点がある人のこと。問題文の用語、聞かれている内容を説明できるか。発想は関係ない。簡単な問題が解けるかとか標準問題が解けるかということでない。問題が解けたから基礎力があるかでないので注意すること。
3.数学科を首席で卒業した僕が考える最強の勉強法【大学受験数学】 とん
教科書を完璧をすること。これから数学をする人。受験勉強を始める人。教科書をなぜ重要か。教科書は完璧すぎる。1冊50~60時間で勉強できた。全部で300時間で勉強できる。半年あれば高校数学は終わる。公式の意味を書いてある参考書はない。定義は教科書にしか書いてない。問題集には定義は書いてない。教科書の定義はしっかり理解する。公式は定義から導かれる。公式の意味を考えられる。微分の意味は接戦の傾きである。演習問題、章末問題は解く。難関大学の場合は公式を証明してみる。直前期には時間的に無理。
4.ゼロから高校数学を学ぶ方法【レベル別・目的別】 とん
高校の教科書を手元におく。受験生・社会人でも大事。教科書以外のテキストは必要ない。わからないところを調べていく。教科書→1対1対応(青チャ-ト スタンダ-ド演習 新数学演習でもいいかも)解答が理解できればその問題集は使える。
5.【参考書:大学への数学】受験合格点に届くために必要なテキストを全紹介 とん
教科書が終わったら参考書1対1対応。どこでも5割はとれる。東大でも5割はとれる。新数学スタンダ-ド演習をやれば5割以上はとれる。問題が多い。これをやるんだった過去問をやる方がいいという場合がある。7割じゃ足りない場合、超難関は新数学演習を勧める。ただし時間はすごくかかる。整数はマスタ-オブ整数をやっとけばいい。整数は一番コスパが悪い。微積分は微積分の極意。
6.数学が出来ない人の特徴【小学生~社会人を指導してみた経験談】とん
数学出来ない。1.計算負荷が高すぎる。何も考えない計算力がベース。2.公式の意味を理解していない。3.考えることを放棄している。自分で考えて解く。考える人は瞬間で伸びる。
7.1+1=2の証明を高校生でもわかるように数学徒が解説してみた【大学数学】とん
ペアノの公理
1.自然数0が存在する。高校までは0は自然数でないというが大学からは0を自然数に入れる。
2.自然数という集合が空ではないとする。
3.任意の自然数にはその後者 suc(a)が存在する。suc(1)=2 suc(3)=4 aの値の入れるとsuc(a)はaは次の値になるとする。
4.0はいかなる自然数の後者でもない。
5. 異なる自然数は異なる後者を持つ
6.aがある性質を満たせばその後者 suc(a)もその性質を満たすときすべての自然数はその性質を満たす。
suc(0)=1 0の後者は1 suc(1)=2 とする。
a=suc(0) b=0 とすると suc(0)+ suc(0)= suc(suc(0)+ 0)
1 + 1 = suc(suc(0))= suc (1)=2
8.大学受験数学の採点基準を数学科首席が翻訳・解説【東大・京大・東工大・東北大・慶應大】とん
東大の採点基準
- 計算力を問う問題、数学的センスを必要とする問題、工夫を必要とする問題、様々な解法がある問題のバランスを配慮している。
- 学習指導要綱に沿っていて、高校の基本的な学習内容の理解と習熟があれば解ける問題の出題を心掛けている。
- 良問であれば、有名問題でも過去問でも繰り返し出題する可能性がある。過去同様の出題があるかは確認しない。
- 数学で差が出るようにして、数学が出来ないのに合格できる可能性を排除する。
- 難問・奇問は避け、潜在的な力を見る。
- 現在の合格ラインには不満がある。
- 採点官による主観の違いが出ないよう、複数人で相談し、常に最大限の注意を払いながら採点している。
- なるべく1つのパターンにはまらない問題を出題したい。すると、本当にさまざまな答案が出るので、採点基準は、他の受験生との比較や全体の印象や問題の趣旨やその他あらゆることに依存して変わってくる。
- 単純に増減表を書いて最大・最小を求めるようなものは出題しない。複雑な条件が絡み、何故最大なのか説明が必要なものは、それがなければ答えがあっていてもかなりの減点になる。
- 最終的な答えとは関係のない部分での計算ミスなども含めて、答案に書いてあるものはすべて目を通し、間違いがあれば減点する。
- 字が薄かったり小さい答案は、細心の注意を払って採点しても見落とす可能性がある。読めないものは、書いてないものと判断する。
- 受験生には、「論理性」と「計算力」を求める。
- 論理を重視し、時間をかけて厳密に採点する。紙に書いてあるものだけで判断する。
- 論証は、日本語できちんと説明して欲しい。論証重視の問題では、式を羅列しただけでは、ほとんど点にならない。
- 論証問題は厳しく採点する基本方針だが、あまり厳しくすると軒並み0点になるので、高校生が限られた時間内で解いていることを配慮して採点する。
- 「a=b」のように式だけを書くのではなく、きちんと日本語で説明をしてほしい。「a=bと仮定した」のか「a=bを代入した」のか「a=bが導かれた」のか。
- 小問がついていることもあるが、最後の問題を解いて欲しい。
- 途中の推論が正しければ、最終的な答えに至らなくても部分点を与える。
- 直感で解いて記述が不足していても、方向性があっていれば部分点を与える。
- 符号を2回間違えて正しい結果に戻ったというような場合も、全ての途中過程をチェックしているが、減点するかは場合による。
- 論理的記述力を見る問題では、答えのみ羅列しても得点は低い。
- 出てきた答えが常識的に正しいかをもっと意識して欲しい。面積が負になっていたり、確率が1より大きくなっていたりするような答案は、できればマイナス点をつけてやりたい。
- 最後の答えがあっているだけで完答できたと考えている受験生が多いが、たいてい満点ではない。
- 予備校の模試の採点は、本番に比べると極めていい加減である。実際は、論理力・表現力を重視して採点しているので、単純にここまでで何点というものではない。
- 立体問題や整数問題は、高校の授業で軽視されているが今後も出題する。
- 面積・体積など答えさえ求まればよい問題では、高校範囲外の知識を用いても問題はない。しかし、使用条件などをチェックせずにいい加減に使っているものがほとんどで、その場合は減点する。
- ロピタルの定理を用いてもよいが、極限値の存在証明を行う必要がある。そもそも、大学の知識で簡単に解けてしまう問題は、出題しないように注意している。
- 「高校範囲外の知識を用いてもよいか」「分母は有理化すべきか」「関数の連続性を断るべきか」など、一律の基準はなく、そのときに拠る。
- 合同式はいきなり使うのではなく、定義を書いてから使ってもらいたい。
- 最大・最小問題において、そのときのxの値は要求されていない限り答える必要はない。
- 文系が分数関数の微分を用いて解答しても問題はない。
京都大学
- 易問から難問までバランスよく出題したい。難問は解けるか解けないか、易問はどう解答するかが問われる。易しい問題でも、小問に分かれていなければ受験生の論理力を試すことが出来る。
- 思考を要する問題だけでなく、ある程度パターン問題も出題し学力を測る。
- 基本的に小問はつけない。部分点を稼ぐより1問の完答を期待する。
- 京大は解法が複数ある問題を好むという印象を持っている人が多いが、様々な解答があると採点が大変になるので特別に意図しているわけではない。
- 教科書の発展にしか書かれていないレベルの内容でも出題する。
- 公表している出題範囲からはすべて出題する。何年か分をまとめてみると全範囲から出題している。
- 問題作成者は毎年全員を入れ替える。
- 傾向がなくなるように工夫して問題を作る。
- 通常の学習の延長線上にあって高校生でも理解できる問題ならば、学習指導要綱を超える内容でも出題する。
- 文系でも出題範囲を広く設定し、理系の範囲を出題していく可能性がある。
- 今後、簡単な微分方程式を出題する可能性がある。
- プロの数学者が中心となって採点するので、細かい手順に違いはあるが採点の基本精神は東大と同じである。
- 答案は2回ずつ時間をかけて丁寧に採点し、説明が不足していないか受験生が理解しているかを確認する。丁寧に部分点を与えるということではなく、丁寧に減点するということであり、受験生に厳しい基準を要求している。
- 論理を重視して採点する。答えが求まっていても説明不足だと半分以下の点しか与えないことも多い。逆に、答えが求まっていなくても論理が正しければ部分点を与える。
- 解答用紙に書いてある考え方は、正答につながるもののみ部分点を与える。部分点狙いでの知識の羅列にはほとんど点を与えない。
- 「この公式を用いればよい」とだけ書いてあっても得点は与えない。
- 数学的帰納法で自明なn=1のときを書いただけでは点を与えない。
- 高校生の知識として明らかとしてよいことと駄目なことに分けて、正確かつ簡潔に記述してほしい。
- 答案には必要なことは全て書き、必要のないことは書かないのが望ましい。
- 式の羅列だけで説明不足の答案は好ましくない。
- 基本的な小問などは0点か満点の2択である。
- 易しい問題では論理の不備や説明不足があると0点になる。
- 高校範囲外の知識を用いても数学的に正しいなら問題ない。ただし、採点基準は相応のものになる。
- 「~であればよい」という表現はそのまま受け取ると十分条件を意味するが、必要十分条件の意味で使っていると思われる答案が多い。言葉の選び方にも注意してほしい。
- 一部のサイトでは「京大は採点が厳しく完答主義で部分点はほとんど与えない」とあるが、実際は受験生の数学力がわかるよう配慮して採点している。
- 見慣れないからといって勝手に難問だと思いこんでいる傾向がある。
- もっと教科書を大切にしてほしい。教科書の理解が100%でないため、いろいろなところでアラが出ている答案が多い。
- 多くのパターンを暗記してきただけのように思える答案が多いのは残念だ。
東京工業大学
- 難問だと差がつかないので、易しめの問題を出題し数学で差がつくようにして数学の出来る学生を採りたい。
- 中途半端な公式やパターンの暗記は害である。無理にでも当てはめようとして不自然な思考に陥ってしまう。
- 過程を大切にし、いかに答えを導いたかで採点する。
- 様々な思考力を見る問題を重視して出題していく。
- 明らかな内容でも何故そうしたかを一言でも説明するべきである。
- 採点官は書いてあるか否かで判断する。内容から推察するようなことはしない。
- ロピタルの定理など高校範囲外の知識でも正しく使えていればよい。しかし、ロピタルの定理は使い方を間違えている受験生が多い。
- 大学1年生を見ているので合格者全員が次の問題を解けるわけではないことを知っている。結果、満点は3割で合格者の数にほぼ等しい。(1)は6~7割が正解。(2)では216通り書き出した受験生がいた。

東北大学
- 問題は10人ほどで数回会議を開いて作り、採点は30人ほどが1週間かけて1人1000枚ほど行う。
- 採点基準は学部で異なる。
- 過去問と同じ問題でも出題する可能性がある。
- 文系の問題は理系の問題に比べて明確に易しくしたい。
- 易問から難問まで知識・計算力・論理力を問う問題をバランスよく出題したい。
- 学習指導要綱の範囲内で出題する。
- 説明や途中計算が不足している解答は答えが合っていても減点する。
- 必要条件と十分条件の認識が甘い答案が多いが、全て減点しているときりがないので黙認することもありうる。
- センター試験と2次試験の相関関係はあまり見られない。
- いわゆる1/6公式などは断りなく使うと減点する。そもそも使用自体好ましくない。
- ロピタルの定理は使うべきではない。
- ケーリー・ハミルトンの定理は断りなく使うと減点する。
- 高校の常識と大学の常識が同じであるとは思わないで欲しい。
-
慶応大学
- 「答案は読みやすいように丁寧に書く」という表紙の注意事項を確認して欲しい。
- 問題にはなるべく図を入れず、受験生が問題から読み取り表現する能力を試したい。
- 易しい問題が多いときは答案をよく見て厳しく採点する。
- 思考力を問うためには全て記述式が望ましいが、時間的制約を考えると穴埋め問題を多く出題せざるを得ない。
- 穴埋め問題は、途中計算は見ずに穴埋めの結果のみで採点する。部分点も与える。
- 記述式では何段階かに分けて加点する。方針が正しければ「方針点」として加点する。
- 「明らか」は使うべきではない。
- 受験生全員が必要条件のみで十分条件の考慮がない場合、必要条件のみでも満点を与える。
- 入学後の実験データの整理で確率の知識が必須となるため、確率は毎年出題していきたい。
-
元東大教授の岡本和夫氏の見解
- 公式についてどれだけ説明すべきかは場合による。
- 入試は大学での学習に十分な力があるかを判定する場であるから、答案が指導要綱に適合しているかはどうでもよい。
- ロピタルの定理は使い方を誤るとバッサリ減点される。この定理嫌い。
- もう一度大学に入り直す人もいるのだから数学的に正しいならば高校範囲外の知識を用いてもよい。実際には答案の流れを見て判断する。とにかく、内容が読み手に伝わり、使い方が正しいことが大切である。
- 採点者は数学のプロなのでごまかしてもすぐにバレる。
- 採点者は「何とか点をあげよう」という優しい人達である。しかし、それができる答案が・・・
- グラフの概形を描く問題で、f”(x)を計算して凹凸を調べる必要があるかは場合による。ただし、雑なグラフは採点者が怒るので、時間次第だがf”(x)も必要だと考えておいたほうがよい。
- 式自体の証明でない限り、計算途中で1/6公式を用いても問題ない。ただし、計算過程の記述が少ない答案はもし答えが違うとバッサリ減点される。
- 外積を用いても数学的に正しいならば問題ない。
- 式自体の証明でない限り、∫logxdx=xlogx-x+C の途中計算を書く必要はない。
- ∫[0→1]√(1-x²)dx=π/4 などは、一言「半径1の円の1/4の面積」と書いておけばよい。答案を書くときは面倒くさがらず、一言でも添えるという姿勢が重要である。
- 答案の書き方の基本は「横書きに書く」「各行は左から右に書く」「行は上から下に続く」のたった3つである。これだけのことが守られていない。
- 答案は丁寧に書いて欲しい。6とbや9とqが区別できないのは困るし、本人も間違えている。
9.大学数学の挫折ポイントBEST3【数学科の自信を砕く難しい分野】とん
大学数学の難点
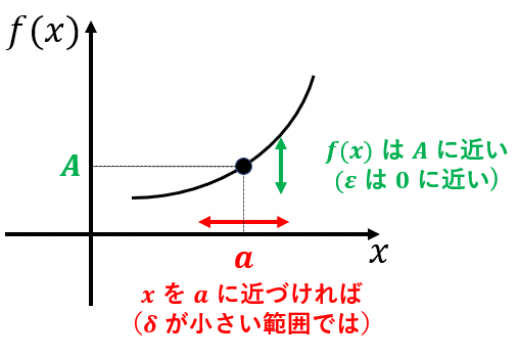
1..ε-Δ法
-
- |x-a| が限りなく 0 に近づくとき,|f(x)-A| が限りなく 0 に近づく
- どんなに小さな正の \varepsilon に対しても |x-a| を十分 0 に近づければ |f(x)-A|<\varepsilon となる
- 任意の正の実数 \varepsilon に対して,ある正の実数 \delta が存在して,0<|x-a|<\delta なら |f(x)-A|< \varepsilon
- 2.位相空間代数的トポロジーという言葉から, 位相空間を研究する分野だと思っている人が多い, ような気がする。開集合族という意味の topology と研究分野としての topology を混同しているからだろう。研究分野としての代数的トポロジーの起源となったのは, Poincaré の Analysis Situs であるが, Poincaré は, 研究対象として多様体を想定していた。 その後, 位相空間の概念が導入され, 更に Eilenberg によりホモロジーが位相空間に対し拡張されたことから, 位相空間を研究対象として考えることができるようになったわけであるが, 中心となるのは, 多様体やCW複体などの扱い易い空間である。
- 3.多様体
- ユークリッド空間をモデルとした位相空間を多様体という。いちばん単純な図形は点であり、これは〇(れい)次元多様体という。線の図形のうち、左右無限に延びている直線、半直線、円周、線分が一次元多様体である(図A)。これに対して図Bのような線の図形は多様体ではない。すなわち、図Bで点Pの近傍、つまり点Pの近くにある点の集合が、(a)では十字形であり、(b)ではT字形であり、どちらにしろ線分ではないからである。面の図形は、その各点で、その近傍が円板と同位相になるものを二次元多様体という。図Cのような、平面や球面や円板やトーラス(輪環面)は様体であるが、球面に矩形(くけい)などを取り付けた(e)のような図形は、取り付けた点Pの近傍が円板でないので多様体ではない。各点の近傍が球体(つまり三次元球体)となるような三次元的図形が三次元多様体で、普通の三次元空間や三次元球体自身はそれぞれ三次元多様体である。同様に、各点の近傍がn次元球体となるようなn次元的図形をn次元多様体という。n次元空間やn次元球体はn次元多様体である。多様体は、平面や球面やトーラスのように境界のないものと、円板のように境界(円板はその円周が境界となる)をもつものとに分かれる。境界のない多様体の各点の近傍は球体からその境界を除いた開球体となる。よって境界のない二次元多様体上に近眼の虫がいると仮定すると、虫はどこにいても同じ開円板(境界の円周を省いた円板)、つまりいつも同じ景色を眺めていることになる。さらに球面やトーラスは空間の中で有限の大きさをもつ閉集合であり、閉じた多様体(二次元の場合、閉曲面)という。多様体が三角形分割できて多面体とみなせるとき、組合せ多様体といい、さらに多様体に微分構造が導入できるとき微分(可能)多様体という。
10.高校数学と大学数学の違いベスト3を数学科生が紹介!【数学科はやめとけ】
大学数学と高校数学の違いは計算量。大学では多変数の多次元の計算がある。次には抽象度。距離。位相での距離。積分はリーマン積分だったがほかにたくさん増える。積分の種類も増える。抽象度を求めないなら数学科にはいかないこと。
11.【ゼロから】数学が苦手な人向けのとっておき勉強法 ゆし
数学が好きになり楽しくなり得意になる。公式や解法を暗記する。例えば三角関数の公式をすべて覚えているか?覚える公式はそれほど多くない。解法の暗記。チャ-トアンドガイドに乗っている。覚えるのはボイスメモで公式で読み上げる。苦手なものは書かずに音で勉強する。なんかいも何回も聞く。勉強したところはすぐボイスメモに取る。
12.10時間以上勉強する3つのコツ ゆし
1.休憩時間 歩きながらする。リラックスするような時間にする がちがちにしない。
2.すきま時間 トイレの時間、風呂の時間、歯磨きの時間、音声教材をたくさん使う。スマホをビニル袋に入れたら簡単にできる。
3.当たり前の基準が違う。10時間勉強することが目標になっている。合格したいという目標でなく10時間の時間が目的になっている。 入学したらというスト-リ-を作る。
「毎日、前向きな気持ちで自然と10時間勉強できてすがすがしい」ということをいう
13.【数学の勉強法】たった1年で国公立に合格する方法 ゆし
高いレベルの参考書はやらない。セルフレクチャ-の勉強法。1つの問題を1分でやる。解法を口でぶつぶつ言う。書くのは最後。最初は解法を暗記する。反復すること。7回反復する。1週目は見るだけ。1周目は早く見る。ざっと見る。
◎できる
○見たときはできないが理解できる。つぎはできる。
△解ける自信がない
×答えを見てもわからない
2回目は見てすぐ解法がわかるか。 3回目は3日以内にする。4回目も同じ。最終的に答えを隠しても答えが言えるか。 セルフレクチャ-は黒で、書くのは赤でと色分けする。6月になったら書いていく。
できない問題 7回以上繰り返し理解できなかった問題が、君の本当に理解できない問題は宝の山 なので、これを先生に聞いて理解できたら、また何度も繰り返すと1冊が完璧になるんじゃないかと思います。
14.【効率10倍UP暗記術!】知るだけで脳が活性化する7つのポイント ゆし
1回やって放置すると忘れてしまう。間をあけずに復習する。昨日のことを今日またやる。次の日は最初の日、また最初からやる。仕訳する。◎知ってる○すぐに言えた。 △知ってるけど言えない××知らないし言えない
◎のところは時間をかけない。例えば白チャ-トでは3日に1回できるようにする。人間の脳はインプットとアウトプットで活性化する。いつでもどこでも音読する。学習効率を高めるのは音読する。耳を使って勉強する(耳勉)。
穴埋め・・・部分的に覚える。虫食い的に覚える。飛ばし飛ばしに覚える。
場所かえ・・記憶した場所から記憶を引き出せる。内容によって覚える場所を変える。場所かえで覚えていた。景色で英単語を覚えていた。
瞑想法・・道順のものでそれを結び付けて覚える。
15.【数学の勉強法】毎日15分で学年1位が取れる!まさかの方法とは?
受験数学は解法を覚えることの方が早い。1冊の参考書を完璧にすること。
16.【医系数学解説1】元祖ビリおじが完全独学で千葉大医学部に合格した数学勉強法
上田亮氏 数学の知識0から千葉大学医学部に合格した数学の勉強方法を紹介しています。高校では数学全く勉強しなかった。過去問10年間集めてやるとだいたい受かる。中学、高校は数学は違う。センタ-試験など撃沈した。合格した年はほぼ満点。何となくわかっていても解答できない。それだけでは合格できない。まずわかること。まず解答を見て正解が確実にできること。反復繰り返しできること。正確に確実にすること。10分の1ですること。実際には5分の1までに短縮することができること。逐次通訳ができること。いちいち書いては時間がない。becauseなんか——これでbecauseとする。理解さえしていれば簡略化できる。sinΘはsΘとする。真面目系な人はノートを作るがこれは必要ない。この方法は邪道であろうが数学の専門家になろうとするので無ければかまわない。
17.社会人が独学で医学部合格した勉強法【医師で同時通訳者上田先生】
数学はどうやったらいいかわからなかった。予想問題を10分の1になるまでやった。試験に出たところをやる。世界史では100点だったが受かればいい。医者になるのに数学はいらない。白チャ-トで十分。化学で酸化還元なんか有機、Z会なんか何回もやった。
17.E判定だった私が京都大学に逆転合格するまでの物語【受験勉強編】ゆし
自分にとって合格することが当たり前と思う。数学が嫌いだった。 高校は進学校だったが280/320ぐらいだった。できるレベルからやっていく。できるところからやっていく。最初は白チャ-トからやっていく。小さいできるを積み重ねていく。合格をつかみ取りに行く。
18.E判定から京都大学に逆転合格!数学の成績が上がった秘訣とは…?ゆし
数学、現代文がうまくいかなかった。数学は波があった。秋から安定した。思考連続法で。過去問をずっと考えた。休憩の時に見ていた。数学の公式のプリントをやった。A判定で安心しない。秋に合格点をとっても安心しない。
19.白チャート1冊で難関大に合格する方法を教えます ゆし
白チャ-トと実力UPで京大合格。白チャ-トを反復する。実際にやってもらうとできない人が多い。関関同立、MARCHでこれで十分。白チャ-トは問題、解答がセット。セルフレクチャ-でする。分厚いが高速でする。口でぶつぶつ言っていく。やり方を口で言っていく。1題1分。できる問題は飛ばしていく。白チャ-トでなく短期集中ゼミがいい。白チャ-トをやる人はまず発展例題は置いといて基礎例題からやる。白チャ-トで偏差値60程度まで伸びる。その上まで行きたいのであれば+実力アップ問題集をやる。白チャ-トは7回程度やる。
20.ダメな自分を100%変えることができる秘訣 ゆし
自分を変えるためには宣言して実行する。なぜ自分はダメなのか。急激な変化は身体が受け付けない。行動していない。それは情報がないか、行動していないかどちらかである。成功体験を積み上げていく。
21.【必見】たった7日で爆伸び!1日1冊勉強法 ゆし
1日1冊勉強できる。苦手は基本的なところがわかっていない。物理は物理のエッセンス。数学は短期集中ゼミExpress 例150題を1日 化学楽々マスタ-化学 基礎1問1答共通テストで8割取れる。
22.京大数学0→80%!京都大学に逆転合格した数学勉強法♪ ゆし
今年は数学4完1半 現役のとき京大数学 0 共通テスト数学30点 本番はⅡB 満点 実力アップ問題集これ以上できないほどやった。100周した。実力アップ問題集1題5分でできるように。過去問は25年分解いた。実力アップと過去問で丁寧にやて来た。
23.国公立数学はこれでOK!マセマ実力UP問題集 ゆし
マセマ実力UP問題集の使い方。夏までに終わらせること。
問題集のやり方。それぞれの問題を解く。わからなければすぐあきらめる。理解できるかどうかで仕訳をしていく。
◎できる
○見たときはできないが理解できる。つぎはできる。
△解ける自信がない
×答えを見てもわからない
3日に1回反復する。2回目以降は解かずに口で言うだけ。手は動かさない。3日に1回反復する。
関連動画【数学】京大数学4完2半!実力UP!問題集使い方3つのポイント
ⅠA142 ⅡB145 Ⅲ135 422題 条件を翻訳する練習をする。1題あたり5分でできるようにする。
【数学】京大入試本番で4完2半!実力アップ問題集の超具体的な使い方
問題を単に暗記してはいけない。何を訊いているかを把握すること。
マセマ 実力UP!問題集 センター6割から始められる二次対策
センタ-5割から始める。2次対応の問題集のとりかかるための問題集。
『実力アップ問題集』のおかげで医学部に合格できた!使い方・勉強法の注意点教えます
手書きとセルフレクチャ-と併用した。計算ミスの内容を日付と内容をかいておく。理解できないところはマーカ-をひいておく。 入試問題は化粧していたり組み合わせしたりしている。反復する。自分解答とどこが違うかを検討する。
24.【京都大学合格】逆転合格インタビュー! 文学部
高3はぼろぼろだった。学校は行きたくなかった。勉強はしていなかった。浪人してセンタ-試験の5年分を丸暗記した。白チャ-トは1冊30分でできた。セルフレクチャ-でこころ掛けたのは問題のスト-リ-を心がけた。センタ-8割。京大数学ダメ。
25.【共通テスト】数学で9割とるための勉強法と参考書 1
集中ゼミ ⅠA ⅡB 過去問 10年分
26.試験本番の京大数学で7割奪取!数学勉強法
本番では70%できた。過去問では90%。6題で2完2半、でだいたい合格できる。実力アップ問題集とプラチカⅢで100題、世界1わかりやすい京大数学100問、マセマの難問、1題あたり5分できるようになる。京大25ケ年。トップで受かる気持ちでやった。
26.試験本番の神戸大医学部と京大総人の参考書
駿台 長岡亮介氏 数学の総合的研究



コメント